Context

There’s a stream running in my backyard. In french, it’s called a “torrent”: a mountain stream characterized by its irregular flow according to the seasons.

The flow is small (~3 l/s). However, being a torrent, its slope is important and respectable water heights can be reached easily.

I would like to build a waterwheel on the stream. Once I have the waterwheel, and can add a small generator and provide (some) electricity to my household. I’m not expecting much (100 watts at the maximum), but I suppose that it could be fun and interesting.

The stream

Topography

The formula for calculating energy from water height is quite simple: $$P = m \times g \times h \times \text{efficiency}$$

As per this formula, power is directly proportional to the flow ($m$) and to the height (sadly, we can’t change gravity on earth). As we can’t neither increase the flow of a stream, we’ll need to build up a good height.

In order to do that, we had to create the topography map of the stream. Romans were way better than me, but the idea is quite simple. You need a good altitude reference. Then, you simply travel along the stream and measure the waterbed to your altitude reference.

In my case, we used a small laser level (consumer GPS are not accurate enough) which gave us a reasonable precision. Using a ruler, we could then measure the slope by measuring the ground to the laser line:

Once entered into a plotter, we can clearly sea the topography of the stream:

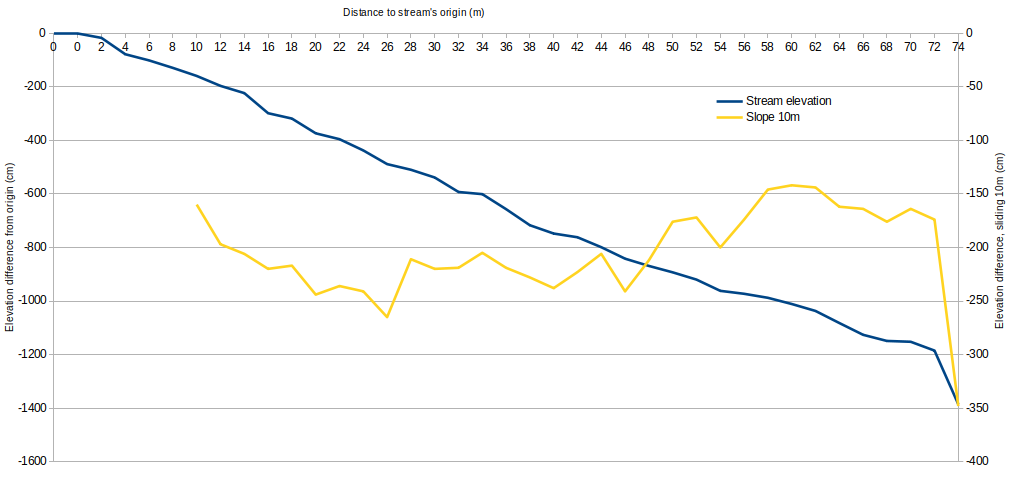
Maximum electricity production

The slope over 10 meters indicates the final slope if the penstock was 10 meters upstream. In my case, if I put the waterwheel at 46 meters from the origin, the 10 meter long penstock will be at a height of 241 cm.

From now, we can calculate the maximum theoretical power that we could have in this configuration: $$Power = 3 kg/s * \text{gravity} * 235cm = 69 W$$

Of course, in real life the turbine, generator, and inverter have (in)efficiencies that need to be taken into account, so the resulting power would be less than $69 W$.

Supposing that the water flows during 9 months of the year, then it would produce at best $69W * 9 \text{month}/\text{year} = 450 kWh/\text{year}$, which if self-consumed, would net us $450 kWh/\text{year} * 0.22 €/kWh = 99 €/\text{year}$

That’s not a lot, by far, but I guess that the interesting side of the project wins over the possible energy production :-)

TBC